Static Trees and Binary Fractions in PostgreSQL
It is not easy to efficiently represent and access trees and other graph structures in relational databases, and this difficulty has motivated the popularity of graph database solutions such as Neo4J. That said, it’s not always practical to set up a dedicated graph database in addition to an existing SQL database instance.
The nested set model is a convenient way to represent trees in SQL. By taking advantage of the set nature of relations, it provides quick and relatively simple queries to determine, for example, all descendants of a given node. Such queries are more computationally intensive using adjacency lists.
The nested set model however, suffers performance penalties on tree updates. Because the nested set model encodes the tree based on the entire tree, when a node is inserted, moved, or deleted, a signficant portion of the nodes must be updated as well (depending on the position of the node). In other words, the encoding depends on the current state of the database. This behavior makes the nested set model less desirable for large, dynamic trees.
A static tree is an alternative to a state-dependent encoding. The materialized path, where nodes 1.1, 1.2, and 1.3 are the first, second, and third children of node 1 is an example of a static tree. Node 1.4 is still the fourth child of node 1 even if there are not four (or more) children of node 1. The encoding value, 1.4, is waiting to be used when the time arises.
With all trees, there are four basic queries:
- What are the children of this node?
- What are the descendants of this node?
- What is the parent of this node?
- What are the ancestors of this node?
And there are the three update operations: inserting a node, deleting a node, or moving a node.
With a static tree, encoding values are predetermined. The node’s position relative to all another nodes is known directly from the encoding value. Given node 1.2.2, we know its parent is node 1.2, and its ancestors are nodes 1.2 and
- We know its children will all have an encoding of 1.2.1.x, and all of its descendants will be prefixed by 1.2.1.
This makes inserts trivial. Inserting a child of a node requires only finding out how many children the node currently has, and giving the new node the encoding appropriate for the next child. If node 1 currently has three children, the new child will have encoding 1.4. No nodes need to be updated when a new node is inserted.
Deleting a node requires finding the nodes of all younger siblings: nodes with the same parent and greater sibling number. Continuing the previous example, if we delete node 1.2, nodes 1.3 and 1.4 become 1.2 and 1.3 respectively. If 1.3 and 1.4 have descendants, we need a way of translating the subtrees of 1.3 and 1.4 to their new positions. This makes translation a fundamental operation when working with trees.
For materialized paths, simply find all of the current descendants of 1.3, and replace the 1.3 with 1.2. This translation is repeated for each younger sibling. Updating is simply translating a node and its subtree to a new inserted position and translating its former younger siblings to fill the hole it left. If the database model requires inserting a node between two existing nodes, just translate the younger siblings to an even younger position.
Materialized paths represented as text in the database makes all tree operations simply a matter of parsing and manipulating strings. In PostgreSQL, one can even create a domain to make sure all paths are properly represented.
CREATE SCHEMA ni;
CREATE DOMAIN ni.path AS
TEXT
NOT NULL
CHECK (VALUE ~ '^([1-9]\d*)(\.[1-9]\d*)*$');One criticism of materialized paths is that string manipulation is undesirable. An encoding that is based on a mathematical algorithm might be better. One possible algorithm is to use binary fractions, which is explained further below. Other algorithms can be used to map the tree as well, such as Farey fractions or continued fractions. Vadim Tropashko has written a number of articles on various nested interval implementations for Oracle using PL/SQL. My implementation is largely a PostgreSQL port of his work using PL/pgSQL. The point of any of these algorithms is to generate a static tree. The only difference is how the tree is encoded and manipulated.
Binary Fractions
The model is called the nested interval model, which implies one dimensional intervals each bounded by two points. However, I think the math is easier to follow if I use two dimensions. If you’re not interested in the math, feel free to skip down to the functions.
Take the unit square described by 0 ≤ x ≤ 1, 0 ≤ y ≤ 1. The goal is to divide this square into progressively smaller, non-overlapping domains, nodes being points represented by (x, y) coordinates. Their position, i.e., which domain they lie within, determines their ancestors, and also the domain of their descendants.
Following Tropashko’s example, let’s place the first node—node 1—at (1, 1⁄2). Where do we place this node’s children? Well, the x-coordinate of the first child of node 1—node 1.1—is the same as its parent, so x1.1 = 1. The y-coordinate of the first child is located at the midpoint of the y-position of the parent (y = 1⁄2) and the depth-first convergence point, where the x-position of the parent meets the diagonal x = y. For node 1, the diagonal intercepts x = 1 at y = 1, so the y-coordiate of the first child is y = 3⁄4: Node 1.1 is located at (1, 3⁄4). You can see that node 1.1.1, the first child of node 1.1, is at (1, 7⁄8), and that 1.1.1.1 is located at (1, 15⁄16).
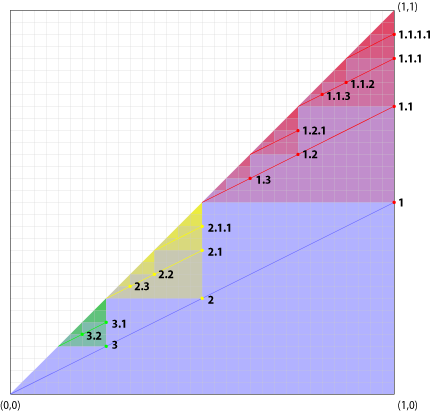
So how about siblings? Siblings are located along the line between the first child and the breadth-first convergence point, where the y-position of the parent intercepts the diagonal x = y. The second child—node 1.2—is located at (3⁄4, 5⁄8). Node 1.3 (the third child) is half-way between node 1.2 and the breadth-first convergence point, at (5⁄8, 9⁄16).
The domain of node 1 is shown in red, and the domains of nodes 2 and 3 are yellow and green, respectively. The depth-first and breadth-first convergence points are simply the points where the lines x = x1 and y = y1 intersect the diagonal: the other two points of the domain triangle.
Also, note that all immediate children of a node z are located vertically half-way between the diagonal and the line y = yz; and horizontally half-way between their next-eldest sibling and the diagonal. This will be useful when finding the parent and sibling number of a given node.
Following this algorithm, we can divide the unit square into smaller and smaller domains, determined by the location of a parent node. In the figure, all children of node 1 are found within the right triangle formed by the diagonal x = y, y = y1, x = x1. In turn, all children of node 1.1 are within the right triangle bounded by the x = y, x = x1.1, y = y1.1.
This fractal pattern continues to infinity, or to the precision of the computer system. As we move deeper into the tree, numbers get big pretty quickly, and quite close together. Accuracy is important, and floating point math is not sufficiently accurate to safely represent the tree. A rational number type which accurately represents integer numerators and denominators is desirable, and something I’d like to implement in PostgreSQL as a base type, but for the time being I’ll represent rational numbers as numerator-denominator integer pairs. Each point is represented by four integers. For example, node 1 is xnum = 1, xden = 1, ynum = 1, yden = 2. I can represent these numerator/denominator pairs in PostgreSQL by creating a type of two BIGINT values.
CREATE TYPE ni.rational AS (num BIGINT, den BIGINT);
CREATE FUNCTION
ni.normalize(in_num BIGINT, in_den BIGINT)
RETURNS ni.rational
IMMUTABLE
STRICT LANGUAGE PLPGSQL AS $body$
DECLARE
v_num BIGINT := in_num;
v_den BIGINT := in_den;
BEGIN
WHILE floor(v_num / 2.0) = v_num / 2.0
LOOP
v_num := v_num / 2;
v_den := v_den / 2;
END LOOP;
RETURN CAST((v_num, v_den) AS ni.rational);
END;
$body$;
CREATE FUNCTION
ni.normalize(in_rat ni.rational)
RETURNS ni.rational
IMMUTABLE
STRICT LANGUAGE SQL AS $body$
SELECT ni.normalize(in_rat.num, in_rat.den);
$body$;| node | x | y | sum |
|---|---|---|---|
| 1 | 1 | 1⁄2 | 3⁄2 |
| 1.1 | 1 | 3⁄4 | 7⁄4 |
| 1.1.1 | 1 | 7⁄8 | 15⁄8 |
| 1.1.1.1 | 1 | 15⁄16 | 31⁄16 |
| 1.1.2 | 7⁄8 | 13⁄16 | 27⁄16 |
| 1.1.3 | 13⁄16 | 25⁄32 | 51⁄32 |
| 1.2 | 3⁄4 | 5⁄8 | 11⁄8 |
| 1.2.1 | 3⁄4 | 11⁄16 | 23⁄16 |
| 1.3 | 5⁄8 | 9⁄16 | 19⁄16 |
| 2 | 1⁄2 | 1⁄4 | 3⁄4 |
| 2.1 | 1⁄2 | 3⁄8 | 7⁄8 |
| 2.1.1 | 1⁄2 | 7⁄16 | 15⁄16 |
| 2.2 | 3⁄8 | 5⁄16 | 11⁄16 |
| 2.3 | 5⁄16 | 9⁄32 | 19⁄32 |
| 3 | 1⁄4 | 1⁄8 | 3⁄8 |
| 3.1 | 1⁄4 | 3⁄16 | 7⁄16 |
| 3.2 | 3⁄16 | 5⁄32 | 11⁄32 |
It should also be obvious from the fact that the algorithm involves repeated halving that these are binary fractions: the denominator is always a power of 2.
Tropashko points out that the x and y values of each node are related and can be equivalently represented as the sum of x and y. Inspection shows that xnum × yden = ynum + 1. For node 1, num1 = 3, den1 = 2, or 3⁄2. These sums will be the basis of the encoding.
Given their sum, we can derive the x and y numerators and denominators using functions. I prefixed my functions with ni for nested interval. The functions take advantage of binary fractions in two ways:
- Adding 1 to or subtracting 1 from a numerator of a fraction in reduced form will give a fraction that is no longer in reduced form. It can be reduced by dividing both the numerator and denominator by two.
- All binary fractions that are not in reduced form can be reduced by repeatedly dividing the numerator and denominator by two until the numerator cannot be evenly divided by two.
CREATE FUNCTION
ni.x(in_rat ni.rational)
RETURNS ni.rational
IMMUTABLE
STRICT LANGUAGE PLPGSQL AS $body$
DECLARE
v_num BIGINT := in_rat.num + 1;
v_den BIGINT := in_rat.den * 2;
BEGIN
RETURN ni.normalize(v_num, v_den);
END
$body$;
CREATE FUNCTION
ni.y(in_rat ni.rational)
RETURNS ni.rational
IMMUTABLE
STRICT LANGUAGE PLPGSQL AS $body$
DECLARE
v_num BIGINT := (ni.x(in_rat)).num * 2;
v_den BIGINT := (ni.x(in_rat)).den * 2;
BEGIN
WHILE v_den < in_rat.den
LOOP
v_num := v_num * 2;
v_den := v_den * 2;
END LOOP;
v_num := in_rat.num - v_num;
RETURN ni.normalize(v_num, v_den);
END
$body$;The two ni coordinate functions.
So, let’s see if it works. I set up a table of the node x-y-sum data.
CREATE TABLE ni_data (
node ni.path NOT NULL UNIQUE,
rat ni.rational NOT NULL
);
CREATE UNIQUE INDEX ni_data_rat_key ON ni_data (rat);
INSERT INTO ni_data (node, rat)
VALUES ('1', (3, 2)),
('1.1', (7, 4)),
('1.1.1', (15, 8)),
('1.1.1.1', (31, 16)),
('1.1.2', (27, 16)),
('1.1.3', (51, 32)),
('1.2', (11, 8)),
('1.2.1', (23, 16)),
('1.3', (19, 16)),
('2', (3, 4)),
('2.1', (7, 8)),
('2.1.1', (15, 16)),
('2.2', (11, 16)),
('2.3', (19, 32)),
('3', (3, 8)),
('3.1', (7, 16)),
('3.2', (11, 32));
/*
node | x | y | sum
---------+-------+-------+-------
1 | 1/1 | 1/2 | 3/2
1.1 | 1/1 | 3/4 | 7/4
1.1.1 | 1/1 | 7/8 | 15/8
1.1.1.1 | 1/1 | 15/16 | 31/16
1.1.2 | 7/8 | 13/16 | 27/16
1.1.3 | 13/16 | 25/32 | 51/32
1.2 | 3/4 | 5/8 | 11/8
1.2.1 | 3/4 | 11/16 | 23/16
1.3 | 5/8 | 9/16 | 19/16
2 | 1/2 | 1/4 | 3/4
2.1 | 1/2 | 3/8 | 7/8
2.1.1 | 1/2 | 7/16 | 15/16
2.2 | 3/8 | 5/16 | 11/16
2.3 | 5/16 | 9/32 | 19/32
3 | 1/4 | 1/8 | 3/8
3.1 | 1/4 | 3/16 | 7/16
3.2 | 3/16 | 5/32 | 11/32
(17 rows)
*/So far, so good!
As I mentioned before, the key to nested intervals is that the entire tree is determined by the algorithm used to generate it. I plotted the children of each node using two rules:
- first child
- xfirst child is midway between xparent and the depth-first convergence point, yfirst child is midway between yparent and the breadth-first convergence point.
- sibling
- xnext sibling is midway between xchild and the depth-first convergence point, ynext sibling is midway between ychild and the breadth-first convergence point.
These rules can also be expressed as functions. The pow function in PostgreSQL
is based on floating point math. Manfred Koizar posted a function
to compute powers of 2 using integers to the pgsql-general mailing list. I have
reproduced his function (with minor editorializing) here and use it in the
functions to calculate the sibling number and parent of a node.
CREATE FUNCTION pow2(in_exp bigint, OUT pow2 bigint)
returns bigint
language plpgsql as $$
DECLARE
v_exp bigint DEFAULT in_exp;
BEGIN
IF (v_exp NOT BETWEEN 0 AND 62) THEN
RAISE '2 ^ % does not fit into a bigint', e;
END IF;
pow2 = 1;
WHILE (v_exp > 0)
LOOP
pow2 = pow2 * 2;
v_exp = v_exp - 1;
END LOOP;
RETURN;
END;
$$;
CREATE FUNCTION
ni.child(in_rat ni.rational, in_child BIGINT)
RETURNS ni.rational
IMMUTABLE
STRICT LANGUAGE sql AS $body$
SELECT CAST((in_rat.num * pow2(in_child) + 3 - pow2(in_child),
in_rat.den * pow2(in_child)) AS ni.rational);
$body$;Let’s see if these worked.
SELECT ni.child(parent, child)
FROM (VALUES ((3, 2)::ni.rational, 1),
((7, 4)::ni.rational, 1),
((7, 4)::ni.rational, 3),
((3, 8)::ni.rational, 2)) AS _ (parent, child);
/*
child
---------
(7,4)
(15,8)
(51,32)
(11,32)
(4 rows)
*/Given the child node, we can find its parent and sibling number. These functions are based on the earlier observation of a child’s position relative to its parent:
- ychild less the vertical distance between the child and the diagonal x = y is equal to yparent.
- Recursively adding the horizontal distance between xchild and the diagonal to xchild will bring you to xparent.
- the number of times of the recursion to xparent is one less than the child number.
CREATE FUNCTION
ni.parent(in_rat ni.rational)
RETURNS ni.rational
IMMUTABLE
STRICT LANGUAGE PLPGSQL AS $body$
DECLARE
k_root_num CONSTANT BIGINT := 3;
v_num BIGINT;
v_den BIGINT;
BEGIN
IF in_rat.num = k_root_num THEN
RETURN NULL;
END IF;
v_num := (in_rat.num - 1) / 2;
v_den := in_rat.den / 2;
WHILE floor((v_num - 1) / 4.0) = (v_num - 1) / 4.0
LOOP
v_num := (v_num + 1) / 2;
v_den := v_den / 2;
END LOOP;
RETURN CAST((v_num, v_den) AS ni.rational);
END
$body$;
CREATE FUNCTION
ni.sibling(in_rat ni.rational, OUT sibling INT)
RETURNS INT
IMMUTABLE
STRICT LANGUAGE PLPGSQL AS $body$
DECLARE
v_num BIGINT := (in_rat.num - 1) / 2;
v_den BIGINT := in_rat.den / 2;
BEGIN
sibling := 1;
WHILE floor((v_num - 1) / 4.0) = (v_num - 1) / 4.0
LOOP
IF v_num = 1 AND v_den = 1 THEN
RETURN;
END IF;
v_num := (v_num + 1) / 2;
v_den := v_den / 2;
sibling := sibling + 1;
END LOOP;
RETURN;
END
$body$;
SELECT node, ni.parent(node), ni.sibling(node)
FROM (VALUES ((11, 32)::ni.rational),
((15, 16)::ni.rational)) AS _ (node);
/*
node | parent | sibling
---------+--------+---------
(11,32) | (3,8) | 2
(15,16) | (7,8) | 1
(2 rows)
*/Comparing with our previous data, we can verify that this is correct.
The dotted path notation is a much more intuitive way to represent the position of the node on the tree than the sum of its x and y coordinates. Here are some functions to convert between the sum and the path and back again.
Note. These implementations rely on the instr function which is ported from
Oracle. It, along with its support functions, can be found in the
PostgreSQL 9.5 Documentation in the
appendix of Porting from Oracle PL/SQL.
CREATE FUNCTION
ni.path_inner(in_rat ni.rational)
RETURNS TEXT
IMMUTABLE
LANGUAGE PLPGSQl AS $body$
BEGIN
IF in_rat IS NULL THEN
RETURN '';
END IF;
RETURN ni.path_inner(ni.parent(in_rat)) || '.' || ni.sibling(in_rat);
END
$body$;
CREATE FUNCTION
ni.path(in_rat ni.rational)
RETURNS ni.path
IMMUTABLE
STRICT LANGUAGE PLPGSQL AS $body$
DECLARE
k_path CONSTANT TEXT := ni.path_inner(in_rat);
BEGIN
RETURN CAST(substr(k_path, 2, length(k_path)) AS ni.path);
END
$body$;The ni_path_inner function returns a string with a leading dot. The ni_path
function is a wrapper which calls ni_path_inner and removes the leading dot.
This is not only for form’s sake: it’s necessary to close the conversion between
path and sum. We want x / y to be equal to
ni_path_numer(ni_path(x, y)) / ni_path_denom(ni_path(x, y)).
SELECT _.node, ni.path(node)
FROM (VALUES ((3, 2)::ni.rational),
((51, 32)::ni.rational),
((15, 16)::ni.rational)) AS _ (node);
/*
node | path
---------+-------
(3,2) | 1
(51,32) | 1.1.3
(15,16) | 2.1.1
(3 rows)
*/
SELECT _.path, ni.node(_.path), ni.path(ni.node(_.path)) AS round_trip
FROM (VALUES (CAST('2.1.1' AS ni.path)),
('1.1.3'),
('3.2'),
('1'),
('3'),
(CAST('3.2' AS ni.path))) AS _ (path);
/*
path | node | round_trip
-------+---------+------------
2.1.1 | (15,16) | 2.1.1
1.1.3 | (51,32) | 1.1.3
3.2 | (11,32) | 3.2
1 | (3,2) | 1
3 | (3,8) | 3
3.2 | (11,32) | 3.2
(6 rows)
*/Distance between two nodes is also useful. The ni_distance function takes two
numerator/denominator pairs in the order distance node1 from
ancestor node2. It recursively walks from node1 to the
root, checking to see if each subsequent parent node2.
Note. I have implemented this straight from Tropashko, including his self-described kludge which returns a large negative number if node1 is not a descendant of node2. This of course would fail to properly return a negative number for deeply nested nodes; in this case if node1 has a depth of 1 million or more. (Though we’ll see later this is unlikely when using this particular implementation.) A more elegant and robust solution is desirable.
CREATE FUNCTION
ni.distance(in_rat1 ni.rational, in_rat2 ni.rational, OUT distance INT)
RETURNS INT
IMMUTABLE
LANGUAGE PLPGSQL AS $body$
BEGIN
IF in_rat1 IS NULL THEN
distance := -99999;
ELSEIF in_rat1 = in_rat2 THEN
distance := 0;
ELSE
distance := 1 + ni.distance(ni.parent(in_rat1), in_rat2);
END IF;
RETURN;
END
$body$;
SELECT _.node1, _.node2, ni.distance(node1, node2)
FROM (VALUES ((7, 4)::ni.rational, (3, 2)::ni.rational),
((31, 16)::ni.rational, (7, 4)::ni.rational),
((7, 4)::ni.rational, (31, 16)::ni.rational),
((15, 16)::ni.rational, (3, 8)::ni.rational)) AS _ (node1, node2);
node1 | node2 | distance
---------+---------+----------
(7,4) | (3,2) | 1
(31,16) | (7,4) | 2
(7,4) | (31,16) | -99997
(15,16) | (3,8) | -99996
(4 rows)With the functions we have so far, it’s possible to build and query a table representing a tree with nested intervals. Let’s take a look at an example of a virtual file system.
CREATE TABLE folders
(
folder_name TEXT NOT NULL UNIQUE,
rat ni.rational NOT NULL UNIQUE
);Note. These ni_ functions work for trees with roots n = 1, 2, 3, … but fail
for root 0 at (1, 0) with sum = 1⁄1.
I’ll choose node 1 as my root, so num/den = 3⁄2.
-- initialize the tree
insert into folders (folder_name, num, den) values ('root', 3, 2);Now, I could calculate the current tree and insert the next folder manually. But a function can do this for us, given the parent folder (node) we want to insert it in. For housekeeping purposes, we’ll fill in the tree sequentially; for example, insert child 1 before child 2. The idea is to count the number of children in of the parent folder n, and insert the new folder as child = n + 1. This won’t work if the tree isn’t filled sequentially.
CREATE FUNCTION
insert_folder(in_parent TEXT, in_new TEXT)
RETURNS VOID
STRICT LANGUAGE PLPGSQL AS $body$
DECLARE
v_rec RECORD;
v_parent_rat ni.rational;
v_child_number INT;
BEGIN
SELECT INTO v_rec
_.rat
FROM folders AS _
WHERE _.folder_name = in_parent;
IF NOT FOUND THEN
RAISE 'Parent folder not found'
USING DETAIL = 'folder_name = ' || quote_literal(in_parent);
END IF;
v_parent_rat := v_rec.rat;
SELECT INTO v_child_number
(COUNT(*) + 1)::INTEGER
FROM folders AS _
WHERE ni.parent(_.rat) = v_parent_rat;
INSERT INTO folders (folder_name, rat)
VALUES (in_new, ni.child(v_parent_rat, v_child_number));
RETURN;
END
$body$;As a convenience, I’ve declared a parent_folder_rational record to hold the
numerator and denominator of the parent folder. I could have used two integer
variables such as parent_folder_num and parent_folder_den instead.
SELECT insert_folder(parent, child)
FROM (VALUES ('root', 'usr'),
('usr', 'local'),
('local', 'src'),
('local', 'pgsql'),
('pgsql', 'bin'),
('pgsql', 'data'),
('pgsql', 'doc'),
('doc', 'html'),
('pgsql', 'include'),
('pgsql', 'lib'),
('pgsql', 'share')) AS folders (parent, child);And let’s create a view to display the folder tree.
CREATE VIEW folder_tree AS
SELECT folder_name, rat,
repeat(' ', ni.distance(rat, (3, 2)::ni.rational))
|| folder_name as folder_name_,
ni.path(rat) as folder_path
FROM folders
ORDER BY folder_path;
SELECT folder_name, rat, folder_name_, folder_path
FROM folder_tree;
/*
folder_name | num | den | folder_rational | folder_name_ | folder_path
-------------+------+------+-----------------+-----------------+-------------
root | 3 | 2 | 3/2 | root | 1
usr | 7 | 4 | 7/4 | usr | 1.1
local | 15 | 8 | 15/8 | local | 1.1.1
src | 31 | 16 | 31/16 | src | 1.1.1.1
pgsql | 59 | 32 | 59/32 | pgsql | 1.1.1.2
bin | 119 | 64 | 119/64 | bin | 1.1.1.2.1
data | 235 | 128 | 235/128 | data | 1.1.1.2.2
doc | 467 | 256 | 467/256 | doc | 1.1.1.2.3
html | 935 | 512 | 935/512 | html | 1.1.1.2.3.1
include | 931 | 512 | 931/512 | include | 1.1.1.2.4
lib | 1859 | 1024 | 1859/1024 | lib | 1.1.1.2.5
share | 3715 | 2048 | 3715/2048 | share | 1.1.1.2.6
(12 rows)
*/Finding the path to a particular folder is the same as finding the ancestors of the node.
-- finding the path to data
SELECT f1.folder_name, ni.path(f1.rat) AS folder_path_x
FROM folders f1
JOIN folders f2 ON ni.distance(f2.rat, f1.rat) >= 0
WHERE f2.folder_name = 'data'
ORDER BY ni.distance(f2.rat, f1.rat) DESC;
/*
folder_name | folder_path
-------------+-------------
root | 1
usr | 1.1
local | 1.1.1
pgsql | 1.1.1.2
data | 1.1.1.2.2
(5 rows)
*/Likewise, finding the subfolders of a particular folder is the same as finding all of the descendants of the node.
-- finding the subfolders of pgsql
SELECT f1.folder_name,
f1.folder_name_,
f1.folder_path AS folder_path_x
FROM folder_tree f1
JOIN folders f2 ON ni.distance(f1.rat, f2.rat) >= 0
WHERE f2.folder_name = 'pgsql'
ORDER BY f1.folder_path;
/*
folder_name | folder_name_ | folder_path
-------------+-----------------+-------------
pgsql | pgsql | 1.1.1.2
bin | bin | 1.1.1.2.1
data | data | 1.1.1.2.2
doc | doc | 1.1.1.2.3
html | html | 1.1.1.2.3.1
include | include | 1.1.1.2.4
lib | lib | 1.1.1.2.5
share | share | 1.1.1.2.6
(8 rows)
*/Updating and deleting nodes requires a bit more work. To delete a node we need to close the hole left by the deleted node if it’s not the last child, which requires moving all of the “younger” children up, and updating all of their children to reflect their new position in the tree. Moving a node involves filling the hole from its old position and inserting it in its new position. If one wants to insert it between two existing children, all of the “younger” children need to be moved further down the line, and their descendants updated. My folder model depends only on parent-child relationships, not child position, so I didn’t implement inserting a node between existing children, but it’s quite straightforward to do so. One reason to do this might be to keep folders in alphabetical order.
The fundamental operation in these updates is relocating a node and its descendants. Before finding the article where Tropashko describes updating the tree, I made my own implementation using paths, being unable to figure out a more elegant method which I knew must exist.
The two functions ni_reroot_numer and ni_reroot_denom simply take the path
to the node to be updated, truncate the path from the old root on up and attach
it to the path to the new root, and then return the numerator and denominator of
the new path. This is where having ni_path and ni_path_numer/ni_path_denom
being proper inverses pays off. This is not the way I’d recommend doing this,
but it does work.
CREATE FUNCTION
ni.reroot(in_node ni.rational, in_old_root ni.rational, in_new_root ni.rational, OUT reroot ni.rational)
RETURNS ni.rational
STABLE
STRICT LANGUAGE PLPGSQL AS $body$
DECLARE
v_node_path ni.path;
v_old_root_path ni.path;
v_new_root_path ni.path;
BEGIN
v_node_path := ni.path(in_node);
v_old_root_path := ni.path(in_old_root);
v_new_root_path := ni.path(in_new_root);
reroot := ni.path_node(v_new_root_path
|| substr(v_node_path,
length(v_old_root_path) + 1,
length(v_node_path) - length(v_old_root_path)));
RETURN;
END
$body$;After finding Tropashko’s follow-up article, I ported his
translation functions to PL/pgSQL. The two complementary functions,
ni_new_numer and ni_new_denom, use two helper functions, ni_normalize_numer
and ni_normalize_denom, to reduce the fractions to simplest form. Functions
described earlier such as the ni_x and ni_y functions could be rewritten to
call the normalization functions rather than include the code inline.
And the ni_new_numer and ni_new_denom functions themselves. They take
advantage of the fact that each subtree is a scaled version of any other, with
the scaling factor k being simply the ratio of the denominators of the old and
new nodes. There are three basic parts to the functions.
- If the node happens to be the old origin, return the new origin.
- For k ≥ 1, i.e., the subtree is “enlarging”, proceed normally. For k < 1, change the operation slightly to use the reciprocal of k, as we need an integer zoom factor for our integer math.
CREATE FUNCTION
ni.new_node(in_node ni.rational, in_old_origin ni.rational, in_new_origin ni.rational)
RETURNS ni.rational
IMMUTABLE
STRICT LANGUAGE PLPGSQL AS $body$
DECLARE
v_zoom_factor INT;
v_num BIGINT;
v_den BIGINT;
v_num_tmp BIGINT;
v_new ni.rational;
BEGIN
IF in_node = in_old_origin THEN
return in_new_origin;
END IF;
IF in_old_origin.den < in_new_origin.den THEN
v_zoom_factor := in_new_origin.den / in_old_origin.den;
v_num := in_node.num - in_old_origin.num * in_node.den / in_old_origin.den;
v_den := v_zoom_factor * in_node.den;
ELSE
v_zoom_factor := in_old_origin.den / in_new_origin.den;
v_num := v_zoom_factor * (in_node.num
- in_old_origin.num * in_node.den
/ in_old_origin.den);
END IF;
v_new := ni.normalize(v_num, v_den);
IF v_new.den < in_new_origin.den THEN
v_num := in_new_origin.num + v_new.num * in_new_origin.den / v_new.den;
v_den := in_new_origin.den;
ELSE
v_num := v_new.num + in_new_origin.num * in_new_origin.den / in_new_origin.den;
END IF;
v_new := ni.normalize(v_num, v_den);
RETURN v_new;
END
$body$;Now we can use ni_new_numer and ni_new_denom as part of a function that
deletes folders and performs the necessary housekeeping operations. It first
checks to make sure the folder to be deleted has no subfolders (this is not a
recursive delete), and that it is not the root node. Then, it finds number of
siblings the folder has and how many are younger. The folder is deleted, and
each younger sibling and its subtree is translated to the next eldest position.
CREATE FUNCTION
delete_folder(in_folder_name TEXT)
RETURNS VOID
STRICT LANGUAGE PLPGSQL AS $body$
DECLARE
v_root_rat ni.rational;
v_rec RECORD;
v_rat ni.rational;
v_child_count INT;
v_sibling_count INT;
v_idx INT;
v_parent ni.rational;
v_child ni.rational;
v_new_child ni.rational;
v_child_number INT;
BEGIN
v_root_rat := (3, 2);
SELECT INTO v_rec
_.rat
FROM folders AS _
WHERE _.folder_name = in_folder_name;
IF NOT FOUND THEN
RAISE 'unknown folder'
USING DETAIL = 'folder_name = ' || quote_literal(in_folder_name);
END IF;
v_rat := v_rec.rat;
IF v_rat = v_root_rat THEN
RAISE 'Cannot delete root folder';
END IF;
SELECT INTO v_child_count
COUNT(*)::INT
FROM folders AS _
WHERE ni.parent(_.rat) = v_rat;
IF v_child_count > 0 THEN
RAISE 'Cannot delete non-empty folder';
END IF;
v_parent := ni.parent(v_rat);
SELECT INTO v_sibling_count
COUNT(*)::INT
FROM folders AS _
WHERE ni.parent(_.rat) = v_rat;
DELETE FROM folders AS _
WHERE _.folder_name = in_folder_name;
IF (v_sibling_count - v_child_number) > 1 THEN
FOR v_idx IN (v_child_number + 1)..v_sibling_count LOOP
v_child := ni.child(v_parent, v_idx);
v_new_child := ni.child(v_parent, v_idx - 1);
UPDATE folders
SET rat = ni.new_node(v_child, v_new_child)
WHERE ni.distance(rat, v_child) >= 0;
END LOOP;
END IF;
END
$body$;And to try it out. I’ll delete the data folder, as it has younger siblings with subtrees which will test to see if these parts of the function work.
SELECT delete_folder('data');
SELECT * FROM folder_tree;
/*
folder_name | num | den | folder_rational | folder_name_ | folder_path
-------------+-----+-----+-----------------+-----------------+-------------
root | 3 | 2 | 3/2 | root | 1
usr | 7 | 4 | 7/4 | usr | 1.1
local | 15 | 8 | 15/8 | local | 1.1.1
src | 31 | 16 | 31/16 | src | 1.1.1.1
pgsql | 59 | 32 | 59/32 | pgsql | 1.1.1.2
bin | 119 | 64 | 119/64 | bin | 1.1.1.2.1
doc | 235 | 128 | 235/128 | doc | 1.1.1.2.2
html | 471 | 256 | 471/256 | html | 1.1.1.2.2.1
include | 467 | 256 | 467/256 | include | 1.1.1.2.3
share | 931 | 512 | 931/512 | share | 1.1.1.2.4
(10 rows)
*/The folder data is gone, and doc, html, include, and share have all
been appropriately updated. The delete_folder function can be modified to
handle moving a folder as well by adding a loop that inserts the folder and its
subfolders into the new location before promoting the siblings.
Limitations
The denominator of binary fractions gets large very quickly, moving through the
available integers at an astonishing rate. Using int4, we’re limited to 29
children for node 1 (1.29 is the youngest possible child), and 29 generations
after node 1 (1.1.1.1.1.1.1.1.1.1.1.1.1.1.1.1.1.1.1.1.1.1.1.1.1.1.1.1.1.1 is the
most deeply nested node possible), with the maximum nesting depth and the number
of children decreasing the with child number and depth: the sum of the numbers
in the path must be less than n − 2, where n is the number of bits
available. Using int8, we can have 62 children of node 1, and 62 generations.
This limitation means there should be additional code which checks the size and
shape of the tree when it’s translated to make sure it will fit in its new
position. This could be done by finding the maximum sum of materialized path
values for each point of the subtree to be moved, and check to see if this and
the sum of the sum of the path values for the new root is less than the maximum.
Tropashko’s nested interval work has been brought up at least twice on the PostgreSQL mailing lists. In March 2004 Manfred Koizar—referring to nested intervals as the Obfuscated Materialized Path Method, or OMPM—wrote he feels nested intervals is “irreparably broken”, its primary failing being that “If you try to store materialized path information in a fixed number of integers you run out of bits very soon.” Tropashko responded (in a post that appears to only have hit the newsgroups) but did not directly address the overflow issue. Looking at other encoding algorithms that may be more efficient with integer use, or at other data types, perhaps there’s still hope. What is needed is an encoding schema that encompasses the range of trees you want to encode. All datatypes and encoding schemes have limitations. The question is whether the limitations restrict what you’re trying to do.
Performance issues have been discussed on the list as well.
The ni_distance function, used to calculated children and parents requires a
full table scan as an index cannot use this information. Alternatives such as
Teodor Sigaev and Oleg Bartunov’s contrib/ltree, Joe Conway’s connectby()
(in contrib/tablefunc), and storing paths directly using strings
and ASCII (as well as the possibility of using bytea) were
mentioned.
There are at least two methods of working around the datatype limitation. Developing a PostgreSQL base type for rational numbers, perhaps based on Perl’s BigRational or other implementation would allow a much larger range of numbers to be used. The availability of a rational data type would also eliminate the necessity of numerator and denominator variants and their accompanying duplicated code. Another alternative is to use a different algorithm for generating the tree, such as Farey fractions or continued fractions, both of which have been explored by Tropashko, who has mentioned in a recent newsgroup point that he is rewriting his article on using the latter. Continued fractions looks particularly promising, and I hope to explore these functions sometime soon.
Code
For your convenience, here are the ni_ functions and the
example data. You will also need to have PL/pgSQL installed in your database
and create the instr functions (with the
appropriate modifictions). The code was developed against
PostgreSQL 7.4.1.
References
- Joe Celko, Trees in SQL
- Vadim Tropashko, Trees in SQL: Nested Sets and Materialized Path
- Vadim Tropashko, Relocating Subtrees in Nested Intervals Model
Reflections
I originally posted this article on 10 July 2004. It was the first—and only!—post on my first blog. I rescued it from the Internet Archive. Looking over the original post there were a number of things I wanted to update. It also provides a snapshot of my writing—both prose and code—and an opportunity to see how these have changed over nearly 12 years.
The original site was generated using Movable Type. Even back then I liked the idea of serving static pages. I used John Gruber’s Markdown and SmartyPants. It’s amazing how Markdown has taken off since those days!
I currently use Jekyll and Markdown, though kramdown has replaced John Gruber’s Perl code. Rather than using a post-processor like SmartyPants, I’m including typographically correct punctuation directly in the text files.
The original post was written when Postgres 7.4 was the current PostgreSQL release and I refer to the upcoming 7.5 release. Due to the number of features added, it was decided to name the next release 8.0 to indicate the significance of the changes. There was no PostgreSQL 7.5.
I also make note of a typo in the PostgreSQL documentation. That typo was fixed shortly after the post was published. Also, the PostgreSQL project moved from CVS to git in September 2010.
My coding style has changed significantly. In particular,
- I no longer use leading commas and add space following commas.
- I aggresively refactor out common code using helper functions after having been first exposed to the DRY principle via the Ruby community.
- I haven’t used aliases since named parameters were introduced (PostgreSQL 8.0)
- I use named OUT parameters (PostgreSQL 8.1).
- I exclusively use dollar quoting (PostgreSQL 8.0)
- I use simple prefixing to distinguish between parameter, variable, and
constant names in PL/pgSQL functions:
-
in_input parameter -
v_variable -
k_constant (taken from a similar practice in Objective-C) - I don’t prefix out parameter names as they are exposed to calling code as part of the API.
-
- I generally use
CASTversus the::operator - I uppercase key words.
- I no longer align parallel code, such as assignments.
- I use
_for vacuous schema aliases. - I now use record types (such as
ni.rational) and variables more extensively since PL/pgSQL support was improved (PostgreSQL 8.0). This makes the separate_numerand_denomfunctions no longer necessary.
I think the new code is much more readable as a result of better coding style and PostgreSQL improvements.
While the original post disappeared a long time ago, I did see that it had some influence. I came across someone using the graphic I created to show the binary fraction domains. When researching this update, I found that it’s used in a couple of slideshare presentations such as this one.